Timsort der Sortieralgorithmus

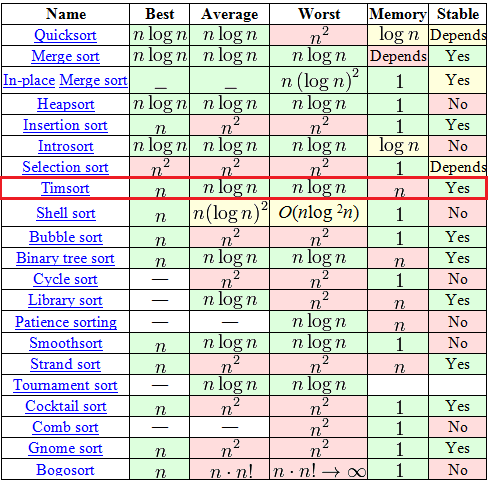
Bei einer scheinbar großen Auswahl an Algorithmen bietet die Tabelle nur sieben passende (mit der O(n logn)-Komplexität als Durchschnitt oder schlimmstem Fall), von denen nur zwei die Stabilität und die O(n)-Komplexität als besten Fall beweisen können. Einer der Beiden ist der gute alte Treesort und der andere ist Timsort.

Der Algorithmus basiert auf der Idee, dass die sortierten Datenfelder in der realen Welt geordnete (egal, wie: ob nicht absteigend oder absteigend) Subfelder enthalten. Und oft ist es wirklich so. Mit solchen Daten ist Timsort allen anderen Algorithmen voraus.

Zur Sache

Bitte erwarten Sie keine komplexen mathematischen Entdeckungen. Die Sache ist, dass Timsort in Wirklichkeit kein eigenständiger Algorithmus ist, sondern ein Hybrid, eine effiziente Kombination aus einer Reihe anderer Algorithmen, gewürzt mit den Ideen des Autors. Der Mechanismus des Algorithmus kann kurz wie folgt erläutert werden:

• Ein bestimmter Algorithmus wird verwendet, um die Datenstruktur bei der Eingabe in Unterfelder zu unterteilen.
• Jedes Unterfeld wird mit einem einfachen Insertionsort
• Die sortierten Unterfelder verschmelzen in einem Array mithilfe von Mergesort. Wie üblich, steckt dabei der Teufel im Detail, nämlich beim Algorithmus in P. 1 und in der Mergesort-Modifikation in P. 3.

Der Algorithmus

Definitionen

• N:Die Länge des Eingabefeldes
• run:Ein geordnetes Unterfeld in dem Eingabefeld. Zur gleichen Zeit ist die Reihenfolge nicht absteigend oder streng absteigend, d. h., “a0 ≤ a1 ≤ a2 ≤ …» oder «a0 > a1 > a2 > …”
• minrun:Wie oben erwähnt, wird das Eingabefeld in dem ersten Schritt des Algorithmus in Unterfelder unterteilt. minrun ist die Mindestlänge eines Unterfeldes. Diese Zahl wird nach bestimmten Logiken aus der Zahl N

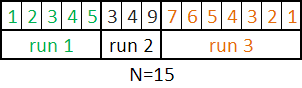
Schritt 0. Minrun-Berechnung.

Die minrun-Zahl wird, basierend auf der N, von den folgenden Prinzipien bestimmt:

• Sie sollte nicht zu groß sein, da die minrun später zum Gegenstand von Insertionsort wird, der bei kurzen Feldern wirksam ist.
• Sie sollte nicht zu klein sein, da, je kürzer das Feld, desto mehr Durchläufe müssen im nächsten Schritt vereinigt werden.
• Es wäre gut, wenn N \ minrun einen Wert von 2 (oder darum herum) hätte. Diese Anforderung ergibt sich aus der Tatsache, dass der Mergesort am besten bei den Feldern von etwa gleicher Länge funktioniert.

Hier bezieht sich der Autor auf seine eigenen Experimente, die zeigen, dass bei minrun > 256 Prinzip 1 nicht erfüllt ist, und bei minrun < 8 Prinzip 2 nicht erfüllt ist, wobei die leistungsstärksten Werte bei 32 bis 65 liegen. Ausnahme: Bei N < 64 ist minrun = N, und Timsort verwandelt sich in einen einfachen Mergesort. An diesem Punkt ist der minrun-Berechnungsalgorithmus so einfach wie ein Stück Kuchen, indem man der N die sechs signifikantesten Bits entnimmt und eins hinzufügt, wenn die übrigen weniger signifikanten Bits mindestens ein einzelnes Bit enthalten. Ein Code dazu wird voraussichtlich etwa wie folgt aussehen:

    int GetMinrun(int n)
    {
        int r = 0;  /* becomes 1 if the least significant bits contain at least one off bit */
        while (n >= 64) {
            r |= n & 1;
            n >>= 1;
        }
        return n + r;
    }

Schritt 1. Unterteilung in Felder und deren Sortierung.

In diesem Stadium haben wir also ein Eingabefeld mit der N-Größe und einer berechneten minrun. Der Algorithmus für diesen Schritt ist folgendermaßen:

• Die Basisadresse des aktuellen Elements ist am Anfang des Eingabefeldes eingestellt.
• Beginnend mit dem aktuellen Array, suchen Sie nach dem run (ein geordnetes Unterfeld) in dem Eingabefeld. Per Definition wird dieses run auf jeden Fall das aktuelle und das darauf folgende Element beinhalten, doch weiterhin ist dies pures Glück. Wenn die endgültige Anordnung absteigend ist, werden die Elemente nicht-absteigend geordnet (Es ist ein einfacher serieller Algorithmus, wir bewegen die Elemente ja nur von beiden Enden hin zur Mitte, indem wir deren Platzierung verändern).
• Wenn das aktuelle run kleiner als die minrun ist, nehmen Sie die Anzahl der Elemente, die dem gefundenen run gleich minrun — size (run) entspricht. Somit wird das endgültige run die Größe von minrun oder mehr haben, wovon ein Teil (im Idealfall alles) geordnet ist.
• Dann wird dieses Feld mit Insertionsort sortiert. Da es klein und teilweise geordnet ist, wird die Sortierung schnell und hochperformant ablaufen.
• Die Basisadresse des aktuellen Elements ist bei dem auf das Feld folgenden Element eingestellt.
• Wenn das Ende des Eingabefeldes nicht erreicht worden ist, gehen Sie zu Punkt 2 zurück, ansonsten ist es das Ende dieses Schrittes.

Schritt 2. Zusammenführung

In dieser Phase liegt ein in Unterfelder unterteiltes Eingabefeld vor. Falls die Daten in dem Eingangsfeld den ungeordneten ähnlich waren, nähert sich die Feldgröße der von minrun, und falls die Daten geordnete Bereiche aufweisen (die Anwendungsanforderung des Algorithmus lässt uns darauf hoffen), übersteigt die Feldgröße die von minrun. Nun müssen diese Felder kombiniert werden, damit wir die endgültige und vollständig geordnete Anordnung erhalten, wofür zwei Anforderungen erfüllt sein müssen:

• Es sollten Felder kombiniert werden, die relativ gleich groß sind (auf diese Weise wird es effizienter sein).
• Die Stabilität des Algorithmus sollte beibehalten werden, d.h. keine nutzlosen Verschiebungen (beispielsweise sollten zwei aufeinanderfolgende gleiche Zahlen nicht vertauscht werden).

Dies wird folgendermaßen erreicht:

• Erstellen Sie einen leeren Paarstapel –. Nehmen Sie sich das erste Feld vor.
• Fügen Sie dem Stapel ein paar Daten –im aktuellen Feld hinzu.
• Beurteilen Sie, ob das aktuelle Feld mit dem vorhergehenden zusammengeführt werden sollte. Um dies zu tun, prüfen Sie, wo die beiden Anforderungen erfüllt sind (angenommen, X, Y und Z sind die drei Top-Felder im Stapel): X > Y + Z Y > Z.
• Wenn eine der Anforderungen nicht erfüllt ist, wird Array Y mit dem kleinsten der Arrays X und Z zusammengeführt. Dieser Schritt wird durchgeführt, bis beide Anforderungen erfüllt oder bis alle Daten geordnet sind.
• Für alle unberücksichtigten Felder konsultieren Sie wieder Punkt 2. Ansonsten war es das.

Das Ziel dieses Verfahrens ist, die Balance zu erhalten, d. h., die Änderungen werden wie folgt aussehen:

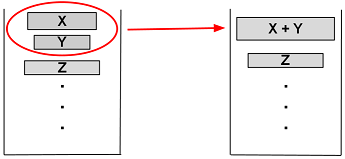
Somit passen die Feldgrößen für die weitere Mergesortierung. Stellen Sie sich den Idealfall vor: Da ist ein Feld mit den Größen 128, 64, 32, 16, 8, 4, 2 und 2 (Vergessen wir für eine Weile die Anforderung, dass die Feldgröße ≥minrun ist). In diesem Fall wird es keine Mengen geben, bis die beiden letzten Felder nicht zusammenkommen, und danach werden sieben perfekt ausbalancierte Mengen gebildet.

Zusammenführung der Felder

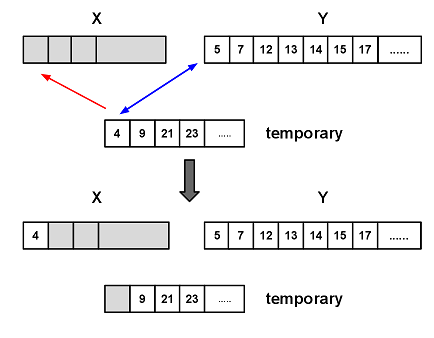
Wie Sie sich erinnern können, haben wir im zweiten Schritt des Algorithmus zwei Felder in einem geordneten zusammengeführt. Die beiden aufeinanderfolgenden Felder werden immer zusammengeführt. Um sie zusammenzuführen, wird zusätzlicher Speicher verwendet.

• Ein temporäres Feld wird mit der kleinsten Größe der zusammengeführten Felder erstellt.
• Kopieren Sie das kürzeste Feld in das temporäre hinein.
• Markieren Sie die aktuelle Position mit den ersten Elementen der großen und temporären Arrays.
• In jedem folgenden Schritt werden die Elemente in den großen und temporären Arrays verglichen und die kleineren werden in einen neu sortierten Array verschoben. Verschieben Sie die Basisadresse des Elements in den Array, wo das Element entnommen wurde.
• Wiederholen Sie den Schritt 4, bis einer der Arrays endet.
• Fügen Sie alle Elemente des verbleibenden Feldes am Ende dem neuen hinzu.

Modifikationen am Mergesort

Alles scheint im obigen Mergesort perfekt zu sein. Mit einer Ausnahme: Stellen Sie sich die Zusammenführung dieser beiden Arrays vor:

A = {1, 2, 3,…, 9999, 10000}

B = { 20000, 20001, …., 29999, 30000}

Das oben beschriebene Verfahren wird auch bei ihnen funktionieren, aber bei jedem vierten Schritt sollte ein Vergleich und eine Verschiebung so durchgeführt werden, dass sie 10000 Vergleiche und 10000 Verschiebungen ergeben. Timsort bietet hier die Modifikation namens Galopp. Sie bedeutet Folgendes:

• Starten Sie den Mergesort wie oben beschrieben.
• Bei jeder Verschiebung eines Elements aus dem temporären oder großen Feld in den letzten wird das Feld aufgezeichnet, dem das Element entnommen wurde.
• Wenn eine Anzahl der Elemente (in dieser Darstellung des Algorithmus entspricht diese Anzahl 7) aus einem und demselben Feld verschoben wurde, kann man davon ausgehen, dass das nächste Element auch aus dem gleichen Feld kommen wird. Um das zu beweisen, wird der Galopp-Modus geschaltet, d.h. Sie gehen das Feld, dasr die nächste Reihe von Daten liefern soll, mit der binären Suche durch (denken Sie daran, dass der Array geordnet ist und wir alle Rechte auf die binäre Suche haben), um das aktuelle Element im dem anderen zusammengeführten Feld zu finden. Die binäre Suche ist effizienter als die lineare, wodurch die Anzahl der Suchvorgänge viel kleiner sein wird.
• Schließlich, wenn die Daten in das zusammengeführte Feld nicht reinpassen (oder das Ende des Feldes erreicht ist), können diese Daten in den Bulk verschoben werden (was effizienter sein kann, als die einzelnen Elemente zu verschieben).

Die Erklärung dazu kann etwas vage ausfallen, lassen Sie uns also einen Blick auf das Beispiel werfen: A = {1, 2, 3,…, 9999, 10000} B = { 20000, 20001, …., 29999, 30000}

• In den ersten sieben Iterationen wurden die Zahlen 1, 2, 3, 4, 5, 6 und 7 aus dem Feld A mit der Zahl 20000 verglichen und, nachdem 20000 als höher eingestuft worden war, wurden sie aus dem Array A in den endgültigen Array verschoben.
• Am Anfang der nächsten Iteration wird der Galopp-Modus eingeschaltet: Die Zahl 20000 wird in der Reihenfolge mit den Zahlen 8, 10, 14, 22, 38, n+2^i, …, 10000 aus dem Feld A verglichen. Wie Sie sehen können, wird die Anzahl solcher Vergleichsschritte weitaus kleiner als 10000 sein.
• Wenn das Feld A leer ist, ist es bekannt, dass es kleiner als das Feld B ist (wir hätten auch irgendwo in der Mitte aufgehört haben können). Die Daten aus dem Feld A sind in das letzte Feld verschoben, und das Verfahren ist wiederholt worden.

Es ist das Ende des Algorithmus.

LESEN SIE AUCH:

• BlueStacks + Eclipse: Debuggen und Testen von Android-Anwendungen beschleunigen
• Überwachung des HTTPS-Datenverkehrs zwischen einem Android-Gerät und einem externen Server
• Code-Review und die Wahrscheinlichkeitstheorie